Optics HW - 1

1.  Review the concept of reflection, particularly the law of reflection.  Draw what happens when a light ray hits a mirror at various angles.

2.  Review the concept of refraction:  what it is, what causes it, what happens during it, under what circumstances does light bend, etc.  Draw what happens when a light ray hits a block of transparent plastic at various angles.  

3.  Show how to calculate the wavelength of WTMD's signal (89.7 MHz).

4.  Some questions related to how light is affected by optics.

Refraction animation

http://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Waves/Refraction/Refraction.html

http://www.animations.physics.unsw.edu.au/jw/light/Snells_law_and_refraction.htm

http://www.freezeray.com/flashFiles/Refraction2.htm

Playing with Light 1 - Reflection and Refraction

Reflection - light "bouncing" off a reflective surface. This obeys a simple law, the law of reflection!

The incident (incoming) angle equals the reflected angle. Angles are generally measured with respect to a "normal" line (line perpendicular to the surface).

Note that this works for curved mirrors as well, though we must think of a the surface as a series of flat surfaces - in this way, we can see that the light can reflect in a different direction, depending on where it hits the surface of the curved mirror. More to come here.

Refraction:

Refraction is much different. In refraction, light enters a NEW medium. In the new medium, the speed changes. We define the extent to which this new medium changes the speed by a simple ratio, the index of refraction:

n = c/v

In this equation, n is the index of refraction (a number always 1 or greater), c is the speed of light (in a vacuum) and v is the speed of light in the new medium.

The index of refraction for some familiar substances:

vacuum, defined as 1

air, approximately 1

water, 1.33

glass, 1.5

polycarbonate ("high index" lenses), 1.67

diamond, 2.2

The index of refraction is a way of expressing how optically dense a medium is. The actual index of refraction (other than in a vacuum) depends on the incoming wavelength. Different wavelengths have slightly different speeds in (non-vacuum) mediums. For example, red slows down by a certain amount, but violet slows down by a slightly lower amount - meaning that red light goes through a material (glass, for example) a bit faster than violet light. Red light exits first.

In addition, different wavelengths of light are "bent" by slightly different amounts. This is trickier to see. We will explore it soon.

Refraction, in gross gory detail

Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).

When the wave enters the new medium it is slowed - the speed becomes lower, but the frequency is fixed. Therefore, the wavelength becomes smaller (in a more dense medium).

Note also that the wave becomes "bent." Look at the image above: in order for the wave front to stay together, part of the wave front is slowed before the remaining part of it hits the surface. This necessarily results in a bend.

The general rule - if a wave is going from a lower density medium to one of higher density, the wave is refracted TOWARD the normal (perpendicular to surface) line. See picture above.

Introduction to Light

Recall that waves can be categorized into two major divisions:

Mechanical waves, which require a medium. These include sound, water and waves on a (guitar, etc.) string

Electromagnetic waves, which travel best where there is NO medium (vacuum), though they can typically travel through a medium as well. All electromagnetic waves can be represented on a chart, usually going from low frequency (radio waves) to high frequency (gamma rays). This translates to: long wavelength to short wavelength.

All of these EM waves travel at the same speed in a vacuum: the speed of light (c). Thus, the standard wave velocity equation becomes:

c = f l

where c is the speed of light (3 x 10^8 m/s), f is frequency (in Hz) and l (which should actually be the Greek letter, lambda) is wavelength (in m).

General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):

Radio

Microwave

IR (infrared)

Visible (ROYGBV)

UV (ultraviolet)

X-rays

Gamma rays

In detail, particularly the last image:

http://hyperphysics.phy-astr.gsu.edu/hbase/ems1.html

http://csep10.phys.utk.edu/astr162/lect/light/spectrum.html

http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg

Don't forget - electromagnetic waves should be distinguished from mechanical waves (sound, water, earthquakes, strings on a guitar/piano/etc.). 

ALL E/M waves (in a vacuum) travel at the SPEED OF LIGHT (c).

The Doppler Effect

http://www.lon-capa.org/~mmp/applist/doppler/d.htm

http://falstad.com/mathphysics.html

Run the Ripple tank applet -

http://falstad.com/ripple/

The key in the Doppler effect is that motion makes the "detected" or "perceived" frequencies higher or lower.

If the source is moving toward you, you detect/measure a higher frequency - this is called a BLUE SHIFT.

If the source is moving away from you, you detect/measure a lower frequency - this is called a RED SHIFT. Distant galaxies in the universe are moving away from us, as determined by their red shifts. This indicates that the universe is indeed expanding (first shown by E. Hubble). The 2011 Nobel Prize in Physics went to local physicist Adam Riess (and 2 others) for the discovery of the accelerating expansion of the universe. Awesome stuff!

http://www.nobelprize.org/nobel_prizes/physics/laureates/2011/

It's worth noting that the effect also works in reverse. If you (the detector) move toward a sound-emitter, you'll detect a higher frequency. If you move away from a detector move away from a sound-emitter, you'll detect a lower frequency.

Mind you, these Doppler effects only happen WHILE there is relative motion between source and detector (you).

And they also work for light. In fact, the terms red shift and blue shift refer mainly to light (or other electromagnetic) phenomena.

Wave questions I and II

Wave questions I

1.  Differentiate between mechanical and electromagnetic waves.  Give examples.

2.  Draw a wave and identify the primary parts (wavelength, crest, trough, amplitude).

3.  Find the speed of a 500 Hz wave with a wavelength of 0.4 m.

4.  What is the frequency of a wave that travels at 24 m/s, if 3 full waves fit in a 12-m space?  (Hint:  find the wavelength first.)

5.  Approximately how much greater is the speed of light than the speed of sound?

6.  Harmonics

a.  Draw the first 3 harmonics for a wave on a string.
b.  If the length of the string is 1-m, find the wavelengths of these harmonics.
c.  If the frequency of the first harmonic (n = 1) is 10 Hz, find the frequencies of the next 2 harmonics.
d.  Find the speeds of the 3 harmonics.  Notice a trend?

7.  Show how to compute the wavelength of WTMD's signal (89.7 MHz).  Note that MHz means 'million Hz."

8.  A C-note vibrates at 262 Hz (approximately).  Find the frequencies of the next 2 C's (1 and 2 octaves above this one).

>

(answers)

1, 2.  See notes.

3.  200 m/s

4.  wavelength is 4 m.  Frequency is 6 Hz.

5.  3,000,000 / 340 --- that's around a million to one ratio

6.

a.  see notes

b.  wavelengths are:  2 m, 1 m, and 2/3 m

c.  frequencies are 10, 20 and 30 Hz, respectively, for n = 1, 2 and 3

d.  speeds are all constant:  20 m/s

7.  speed of light divided by 89.7 MHz.  That is 300,000,000 / 89,700,000, which works out to around 3.3 m.

8.  524 Hz and 1048 Hz

>

Wave questions II

Consider the musical note G, 392 Hz.  Find the following:

1.  The frequencies of the next two G's, one and two octaves above.

2.  The frequency of the G one octave lower than 392 Hz.

3.  The frequency of G#, one semi-tone (piano key or guitar fret) above this G.

4.  The frequency of A#, 3 semi-tones above G.

5.  The wavelength of the 392 Hz sound wave, assuming that the speed of sound is 340 m/s.

6.  What are the differences between longitudinal and transverse waves?  Gives examples of each.  What type of wave is sound?


Also for your consideration.  Understand the following concepts:

a.  harmonics on a string

b.  how waves form in a tube - what actually happens with the air inside?

c.  Here's a thought question for you - why does breathing in helium make your voice higher?

answers:

1.  392 x 2; 392 x 4

2.  392/2

3.  392 x 1.0594

4.  392 x 1.0594 x 1.0594 x 1.0594  (or 392 x 1.0594^3)

5.  340/392

6.  See notes.

Music

In western music, we use an "equal tempered (or well tempered) scale."  It has a few noteworthy characteristics;

The octave is defined as a doubling (or halving) of a frequency.

You may have seen a keyboard before.  The notes are, beginning with C (the note immediately before the pair of black keys):

C

C#

D

D#

E

F

F#

G

G#

A

A#

B

C

(Yes, I could also say D-flat instead of C#, but I don't have a flat symbol on the keyboard.  And I don't want to split hairs over sharps and flats - it's not that important at the moment.)

There are 13 notes here, but only 12 "jumps" to go from C to the next C above it (one octave higher).  Here's the problem.  If there are 12 jumps to get to a factor of 2 (in frequency), making an octave, how do you get from one note to the next note on the piano?  (This is called a "half-step" or "semi-tone".)

The well-tempered scale says that each note has a frequency equal to a particular number multiplied by the frequency that comes before it.  In other words, to go from C to C#, multiply the frequency of the C by a particular number.

So, what is this number?  Well, it's the number that, when multiplied by itself 12 times, will give 2.  In other words, it's the 12th root of 2 - or 2 to the 1/12 power.  That is around 1.0594.

So to go from one note to the next note on the piano or fretboard, multiply the first note by 1.0594.  To go TWO semi-tones up, multiply by 1.0594 again - or multiply the first note by 1.0594^2.  Got it?

Harmonics revisited.

The above picture represents "harmonics" on a string - waves that form and give the maximum possible amplitude.  A string can vibrate at any frequency, but certain frequencies will make the wave BEST vibrate - with the greatest height/amplitude.  These waves are called harmonics and they occur at frequencies which are integer multiples of the lowest possible "resonant" frequency.  For example, if the frequency will produce a simple 1 "hump" pattern (n = 1) at 10 Hz, the next harmonic (2 "humps" or n = 2) will be at 20 Hz.  The next harmonic (n = 3) is at 30 Hz, and so on.

Another way to put it:

Harmonics are a specific case of waves "interfering" with each other – making “standing waves” or “harmonics.” Here we see that certain frequencies produce larger amplitudes than other frequencies.  There is a lowest possible frequency (the resonant frequency) that gives a “half wave” or “single hump”. Every other harmonic has a frequency that is an integer multiple of the resonant frequency. So, if the lowest frequency is 25 Hz, the next harmonic will be found at 50 Hz – note that that is 1 octave higher than 25 Hz. Guitar players find this by hitting the 12^th fret on the neck of the guitar. The next harmonics in this series are at 75 Hz, 100 Hz and so on.

Sound waves are mechanical - that is, they require a medium.  There can be NO sound where there is no medium through which to travel.  That makes them very different from light (or any e/m waves).

Also note that it is easy to calculate the wavelength of a harmonic.  The formula is:

wavelength = 2 L / n

That means, it is twice the length of the string divided by the harmonic number.


Useful terms in music:

In music, the concept of “octave” is defined as doubling the frequency. For example, a concert A is defined as 440 Hz. The next A on the piano would have a frequency of 880 Hz. The A after that? 1760 Hz. The A below concert A? 220 Hz. Finding the other notes that exist is trickier and we’ll get to that later.

Interference:

Waves can “interfere” with each other – run into each other. This is true for both mechanical and e/m waves, but it is easiest to visualize with mechanical waves. When this happens, they instantaneously “add”, producing a new wave. This new wave may be bigger, smaller or simply the mathematical sum of the 2 (or more) waves. For example, 2 identical sine waves add to produce a new sine wave that is twice as tall as one alone. Most cases are more complicated.

In music, waves can add nicely to produce chords, as long as the frequencies are in particular ratios. For example, a major chord is produced when a note is played simultaneously with 2 other notes of ratios 5/4 and 3/2. (In a C chord, that requires the C, E and G to be played simultaneously.) Of course, there are many types of chords (major, minor, 7ths, 6ths,…..) but all have similar rules. In general, musicians don’t remember the ratios, but remember that a major chord is made from the 1 (DO), the 3 (MI) and the 5 (SO). It gets complicated pretty quickly.

Harmonics in tubes - also, transverse and longitudinal waves:

I will demonstrate this in class.  Here are relevant sites which show longitudinal waves (as well as transverse waves).  You know the difference between mechanical and EM waves - mechanical waves need a medium, but EM waves do not (though they can travel in many different mediums, but at a speed less than the speed of light).  Waves can also be classified according to shape:  transverse (standard-looking waves, like sine waves, which move perpendicular to the direction of wave travel.  Longitudinal waves move parallel to the direction of wave travel.  The animations below show this better than words can express:

http://www.acs.psu.edu/drussell/Demos/waves/wavemotion.html

http://www.animatedscience.co.uk/blog/wp-content/uploads/focus_waves/tl-wave.html

Note that light is a transverse wave, but sound is a longitudinal (or compression) wave.

Waves!

So - Waves.....  

We spoke about energy.  Energy can, as it turns out, travel in waves.  In fact, you can think of a wave as a traveling disturbance, capable of carrying energy.

There are several wave characteristics (applicable to most conventional waves) that are useful to know:

amplitude - the "height" of the wave, from equilibrium (or direction axis of travel) to maximum position above or below

crest - peak (or highest point) of a wave

trough - valley (or lowest point) of a wave

wavelength (lambda - see picture 2 above) - the length of a complete wave, measured from crest to crest or trough to trough (or distance between any two points that are in phase - see picture 2 above).  Measured in meters (or any units of length).

frequency (f) - literally, the number of complete waves per second.  The unit is the cycle per second, usually called:  hertz (Hz)

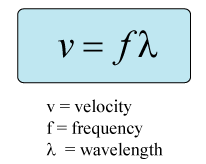
wave speed (v) -  the rate at which the wave travels.  Same as regular speed/velocity, and measured in units of m/s (or any unit of velocity).  It can be calculated using a simple expression:

There are 2 primary categories of waves:

Mechanical – these require a medium (e.g., sound, guitar strings, water, etc.)

Electromagnetic – these do NOT require a medium and, in fact, travel fastest where is there is nothing in the way (a vacuum). All e/m waves travel at the same speed in a vacuum (c, the speed of light):

c = 3 x 10^8 m/s

First, the electromagnetic (e/m) waves:

General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):

Radio

Microwave

IR (infrared)

Visible (ROYGBV)

UV (ultraviolet)

X-rays

Gamma rays

In detail, particularly the last image:

http://hyperphysics.phy-astr.gsu.edu/hbase/ems1.html

http://csep10.phys.utk.edu/astr162/lect/light/spectrum.html

http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg

Mechanical waves include:  sound, water, earthquakes, strings (guitar, piano, etc.)....

Again, don't forget that the primary wave variables are related by the expression:

v = f l

speed = frequency x wavelength

(Note that 'l' should be the Greek symbol 'lambda', if it does not already show up as such.)

For e/m waves, the speed is the speed of light, so the expression becomes:

c = f l

Note that for a given medium (constant speed), as the frequency increases, the wavelength decreases.

Let us examine "harmonics", visible on a string (as demonstrated in class).  Harmonics are wave shapes produced that have a maximum amplitude under given conditions (tension in string, length of string, composition of string, etc.).  Every stretched string has a particular lowest frequency at which it will naturally resonate or vibrate.  However, there are also higher frequencies that will also give "harmonics" - basically, pretty wave shapes.  These higher frequencies are integer multiples of the lowest frequency.

So, if the frequency of the lowest frequency is 10 Hz (for an N = 1 harmonic), the next harmonic (N = 2) occurs at 20 Hz.  N = 3 is at 30 Hz, and so on.

So, what is energy?

I stole my energy story from the famous American physicist Richard Feynman. Here is a version adapted from his original energy story. He used the character, "Dennis the Menace." The story below is paraphrased from the original Feynman lecture on physics (in the early 1960s).

Dennis the Menace

Adapted from Richard Feynman

Imagine Dennis has 28 blocks, which are all the same. They are absolutely indestructible and cannot be divided into pieces.

His mother puts him and his 28 blocks into a room at the beginning of the day. At the end of each day, being curious, she counts them and discovers a phenomenal law. No matter what he does with the blocks, there are always 28 remaining.

This continues for some time until one day she only counts 27, but with a little searching she discovers one under a rug. She realizes she must be careful to look everywhere.

One day later she can only find 26. She looks everywhere in the room, but cannot find them. Then she realises the window is open and two blocks are found outside in the garden.

Another day, she discovers 30 blocks. This causes considerable dismay until she realizes that Bruce has visited that day, and left a few of his own blocks behind.

Dennis' mother removes the extra blocks, gives the remaining ones back to Bruce, and all returns to normal.

We can think about energy in this way (except there are no blocks!). We can use this idea to track energy transfers during changes. We need to be careful to look everywhere to ensure that we can account for all of the energy.

Some ideas about energy

• Energy is stored in fuels (chemicals).
• Energy can be stored by lifting objects (potential energy).
• Moving objects carry energy (kinetic energy).
• Electric current carries energy.
• Light (and other forms of radiation) carries energy.
• Heat carries energy.
• Sound carries energy.

But is energy a real thing?  No, not exactly.  It is a mathematical concept, completely consistent with Newton's laws and the equations of motion.  It allows us to see that some number (calculated according to other manifest changes - speed, mass, temperature, position, etc.) remains constant before and after some "event" occurs.

How things fly!

The amazing science of flight is largely governed by Newton's laws.

Consider a wing cross-section:




Air hits it at a certain speed.  However, the shape of the wing forces air to rush over it and under it at different rates.  The top curve creates a partial vacuum - a region "missing" a bit of air.  So, the pressure (force/area) on top of the wing can become less than the pressure below.  If the numbers are right, and the resulting force below the wing is greater than the weight of the plane, the plane can lift.

This is often expressed as the Bernoulli Principle:

Pressure in a moving stream of fluid (such as air) is less than the pressure of the surrounding fluid.

The image above shows another way to think of flight - imagine the wing first shown, but slightly inclined upward (to exacerbate the effect).  There is a downward deflection of air.  The reaction force from the air below provides lift and the lift is proportional to the force on the wing.

In practice, it works out (in general) to be:

Lift = 0.3 p v^2 A

where p is the density of air, v (squared) is the speed of the plane, and A is the effective area.  Note that the lift is proportional to the speed squared - so, the faster the plane goes, the (much) easier it is to take flight.


Some related animation:

http://physics.stackexchange.com/questions/13030/why-does-the-air-flow-faster-over-the-top-of-an-airfoil

exam 1 topics

General topics for exam 1.  Be sure to review all assigned homework, blog posts and your notes.

You are permitted to have a sheet of notes for this test.  I will NOT give equations.

SI units (m, kg, s) - meanings, definitions
velocity
average vs. instantaneous velocity
acceleration
related motion problems using the formulas
speed of light (c)
gravitational acceleration (g)
freefall problems
Newton's 3 laws - applications and problems
Kepler's 3 laws - applications and problems
epicycles
Newton's law of universal gravitation (inverse square law)
weight vs. mass
center of mass/gravity